I’ve been involved in an interesting exchange of ideas over the past couple of days with Tony Northrup about the effective focal length of Canon’s 70-200mm f/2.8L IS II lens when it is focused at distances closer than its infinity setting (ie, focus breathing). We’ve been coming up with wildly different numbers (mine were presented in a video last month), and we don’t have many outside sources to check ourselves against… perhaps because making the calculation is not a very straight forward process. So, if you’ve ever had the desire to see how your lenses really measure up or how much they breath, here’s how I do it, with a few of the tools that I use to make it faster.
[Update: 10/4/2022] I have updated this article to show a method that is more intuitively easy to understand, and which attempts to measure the angle of view of a lens rather than a focal length directly.
I’d also love to hear your results from using other methodology, and your explanations of those methods. It would be great if I could find a testing method that’s easier than this and just as accurate or better.
Setup
To begin, mount your camera on a tripod near a wall or other vertical surface. Measure from the center of your camera’s sensor to the floor (you can use the vertical center of the lens mount). We’ll call this H. Then, tape something like a metric precision ruler (or metric measuring tape, depending on how wide the lens is) vertically to the wall, with the low end at the exact height of the center of your camera’s sensor from the floor (H). This is just to set up the square angle of a triangle. It’s also important to make sure that the camera is vertically aligned with the ruler.
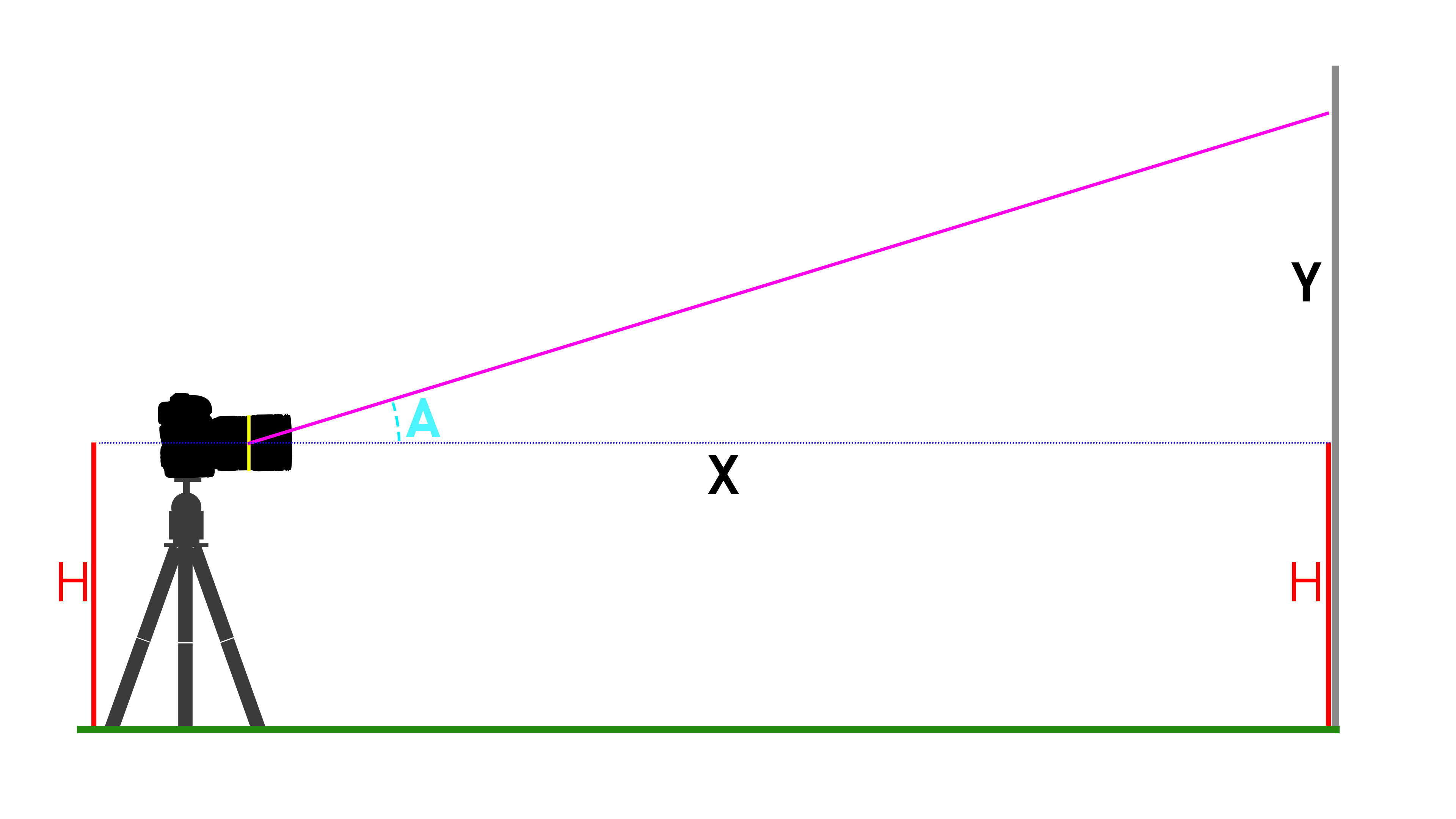
Once that’s done, center your middle focus-point on the end of the ruler. Since your AF point is most likely a rectangle, the end of the ruler should bisect it, dividing it in half (if your ruler’s scale doesn’t start right at the end of the ruler, then center the first markings on the scale in the center of the AF point instead).
Distance From Lens’s “Entrance Pupil” To Subject
First, determine the location of your lens’s entrance pupil (described below), and then measure that distance to the wall (X in the diagram above) I like to use a precise laser measuring tape. My Bosch GLM 50 is accurate to about 1.5mm, but some others are even better. If you’re careful and have some help, a tape measure will also work, though with reduced accuracy.
We’ll call that measurement X.
What’s the Entrance Pupil?
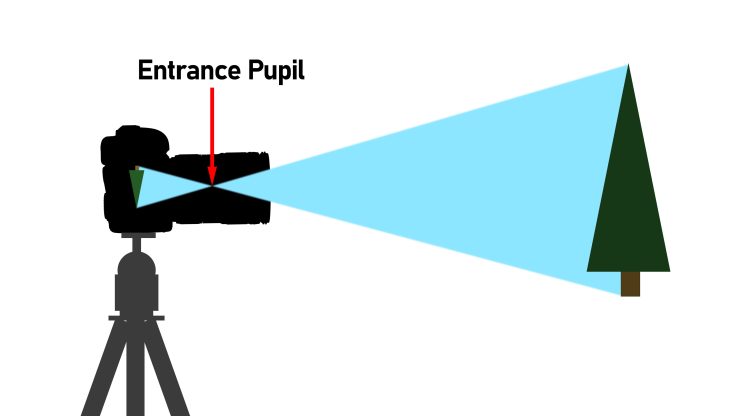
In 2016 I had an email discussion with the great Pierre Toscani who really clarified the matter of where to make the camera-side measurement for me. The entrance pupil of the lens is the point where the angle of view begins, and unless you have a lot of technical data about the lens formula of the lens in question and are adept at ray-tracing, it is best to find it via experimentation.
Landscape photographers often know the entrance pupil as the “Nodal Point” of the lens, and use nodal rails on their camera when shooting panoramas. If you’re shooting a panorama and the pivot point of your camera is directly below the entrance pupil / nodal point, then you’ll avoid parallax problems. Although finding the nodal point is relatively simple, it’s beyond the scope of this article, but there are numerous good tutorials out there already.
Vertical Measurement
Now, focus the camera and take a photo. If your setup is not completely rigid, take several photos to ensure that the exact center of the image is over the end of the ruler scale.
Next, load the image into Photoshop. Create a horizontal guide at 50%. That line should match the beginning of the ruler’s scale in the image. From there, it’s simple: look at the top border of the image and read where the ruler leaves the frame. That measurement is the opposite side of the triangle, which we’ll call Y.
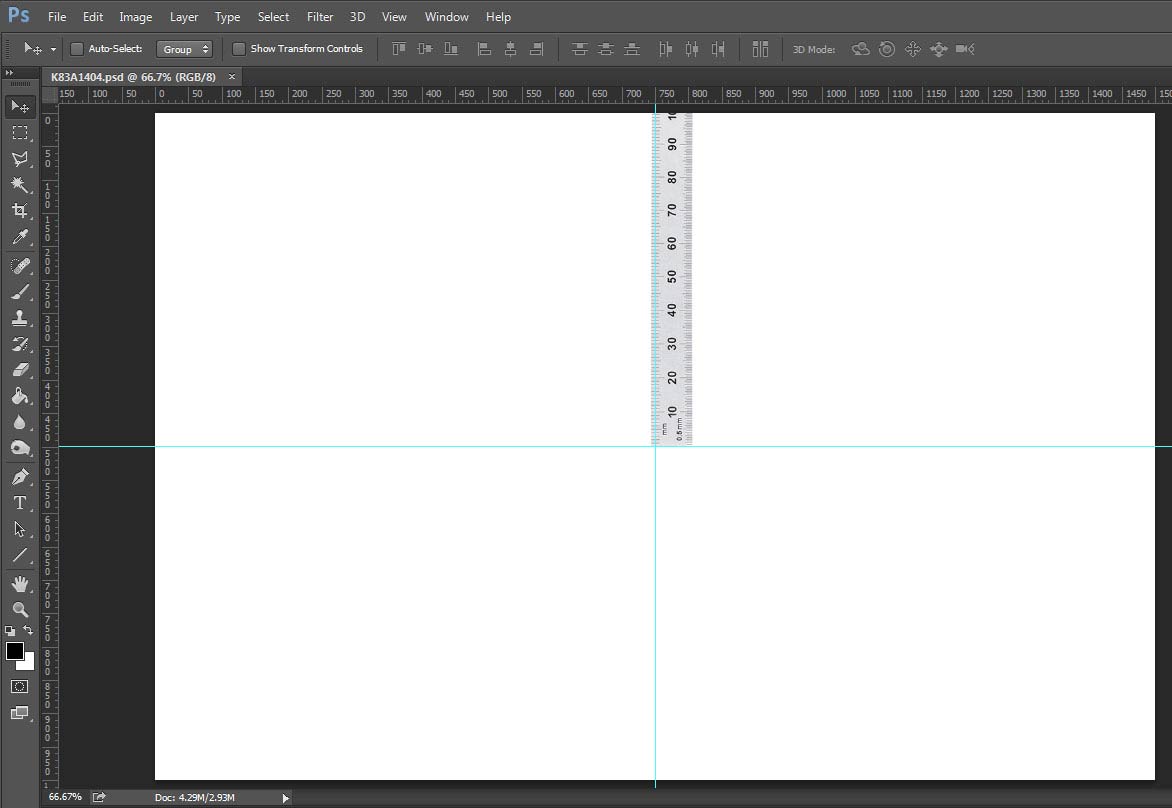
If that guide didn’t match up with the beginning of the ruler’s scale, then adjust your camera and re-shoot or, if you’re comfortable with the ruler tool in Photoshop, figure out how far away the guide is from the start of the scale, and add or subtract that amount. You can avoid using the ruler tool or making estimates by centering your AF point at the 10cm mark rather than the very end, and then subtracting 100mm (plus or minus adjustments) from your final measurement, but since that adds in another opportunity for errors to creep in to the process, I prefer starting at 0.
Calculate the Angle
If you remember your geometry, this is pretty easy, but it’s even easier using an online calculator, like this one at EasyCalculation.com.
Set the drop-down menus so that it calculates angle and hypotenuse side, though we only need angle.
In the fields below, enter your X measurement for adjacent side, and your Y measurement for opposite side, and press “calculate”. That will give you an the angle we need. We’ll call it A.
Get the Focal Length
Once you have found A, you have half of the vertical angle of view of lens, so to get the complete angle of view, just double it. From there, the easiest course it to look up the corresponding focal length based on that angle; there are numerous standardized tables of such things all over the internet, and also tools that will do the exact calculation.
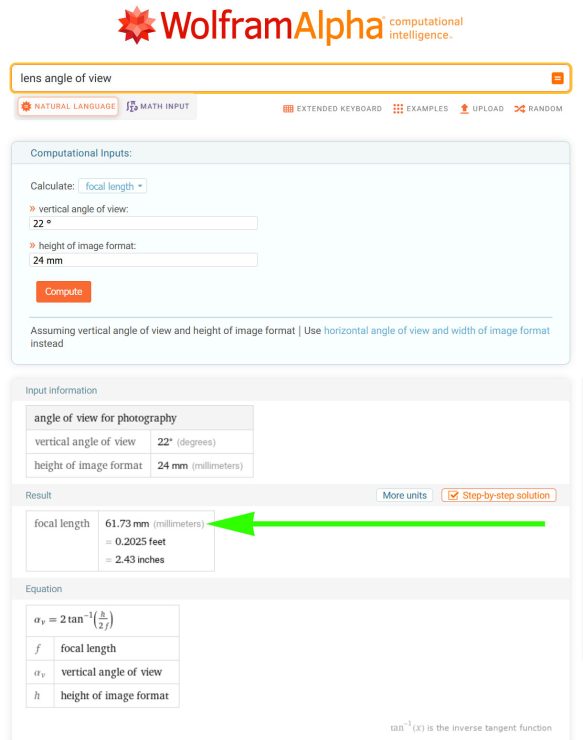
My favorite of these is Wolfram Alpha, which is accurate and flexible. Click here to see Wolfram Alpha’s “Lens Angle of View” calculation page.
In the default example, the calculation assumes that we’re measuring using a vertical angle (which we are) and a full frame 35mm sized sensor (36 x 24mm). If you’re using an APS-C camera or another size, enter the vertical size of the sensor instead of 24mm. So, in the computational inputs, enter the angle of view (A) that we found above in the computational input, and press “compute”.
So, if you found an angle of 22 degrees, then the calculation will return 61.73mm as a focal length. Wolfram is an education site, so you can get a full, step-by-step solution if you want one, too.
Further Support
Visual: Over the past week, I’ve been looking at a couple of different ways to cross-check my measurements and make sure that what I’m getting makes sense. If you’ve seen my video comparison of the Canon and Tamron lenses and their breathing, you’ve seen a clip from Matt Granger’s video on the subject that shows the effect of breathing on his model while shooting video. It’s a simple, visual comparison but it shows what you’d expect: as the Tamron and Nikon lenses are focused towards the MFD, the subjects get smaller, but on the Canon, the subject gets larger.
I wanted a way to quantify this visual change, and Bob Atkins’ article on focus breathing gave me the idea for a way to do it. He used stars as subjects, but I live in Seattle, so that’s not a practical option (hello cloudy skies). So, instead, I used two small LED lights and did this:
I took an under-exposed photo, shot at f/22 (to cut down on bokeh/circle of confusion) with the camera sensor about 26 feet away from the lights, with the lens focused at that distance. The lens, incidentally, was the Canon 70-200 f/2.8L non-IS, since I had read that it behaves similarly to the IS II, but I hadn’t measured it for myself yet. It looked like this:

I then focused the lens to about 12 feet away (using the range indicator on the lens) but did not move the camera. The idea here is to get the same effect as Matt Granger’s racking the focus of his lens in his video, but at some distances that I could measure.
I then took a shot with the lens focused at 7 feet and at 5 feet.
The results can be seen in this GIF:

As you can see, I loaded those images into Photoshop, set guides to mark the centers of each light (easier than I expected to get within a few pixels of the center) and then used the ruler tool to measure the distance from center to center. Those distances are marked on the images above.
Even without the numbers, though, it’s plain to the eye that the lights are getting further apart; the distances involved are not especially subtle. This can be seen simply by looking through the lens and racking the focus. (Note that the CENTERS of the lights are getting further apart, not just the the edges. If I had simply opened the aperture to increase the size of the blur, we’d see results mimicking what you’d expect from zero focus breathing).
But we can look at the numbers, too, so here they are in table form:
| Distance (pixels) | % of 4041 |
|---|---|
| 4041 | 100% |
| 4230 | 104.68% |
| 4524 | 111.95% |
| 4910 | 121.50% |
After doing this, I went back and measured the focal length of the lens at each of these distances from the subject using the original method that I outlined above. My measured focal lengths were:
| Measured Focal Length @ 26, 12, 7, and 5 feet | % of 199.6mm |
|---|---|
| 199.6mm | 100% |
| 206.2mm | 103.3% |
| 216.0mm | 108.2% |
| 248.9mm | 124.7% |
Now, take a look at how these two sets of numbers compare.
| Distance (pixels) | % of starting point | Focal Length | % of starting point |
|---|---|---|---|
| 4041 | 100% | 199.6mm | 100% |
| 4230 | 104.68% | 206.2mm | 103.3% |
| 4524 | 111.95% | 216.0mm | 108.2% |
| 4910 | 121.50% | 248.9mm | 124.7% |
They’re not a perfect match, of course, but part of that reason is that there was a lot of room for slop in this second measurement; I had to set the focus to 7 feet by looking at the range indicator window on the lens rather than by actually focusing on something, for example. But they’re still pretty close… the worst difference is about 3.75%.
This means that from our two different methods, one in which the camera is a stationary 26 feet from the target and one in which the camera is moved to as close as 5 feet from the target, the numbers support each other pretty nicely.
Some people have claimed that the Canon 70-200 f/2.8L and IS II do not breath at all. If that were the case, then both of these sets of measurements would have to be off by at least 20% at the 5 foot mark, but hardly at all at the 26 foot end!
Questions? Problems?
I’ve measured a several lenses this way, each lens multiple times, and the numbers have all come out as I’d expected (after a brief moment of confusion in one case). It’s not my formula, but the equation is simple enough, and certainly makes sense to me. That said, I’m certainly open to the possibility that there’s a mistake or that it’s missing something that would make it more accurate. If it is, and you can explain it to me, I’d be very grateful. Please let me know in the comments below!
On the other hand, if I’ve been unclear about some step in the procedure above, feel free to ask. Good luck!




